Mokssi's repository

리뷰 논문: Deep Adaptive Input Normalization for Time Series Forecasting
https://arxiv.org/abs/1902.07892

Introduction

딥러닝에서 데이터 전처리는 필수적인 단계이다. 아웃라이어, 측정오류 등 사전에 데이터를 가공하지 않으면 성능에 큰 문제가 발생할 수 있기 때문이다. 그 중에서 데이터의 분포, modality 로 인해 딥러닝의 성능이 좌우되는 경우가 많다. uni-modal 한 환경이라면 큰 문제가 되지 않지만, real data 들은 multi-modal 한 경우가 대부분이기 때문에 이를 위한 전처리가 필수다. 특히 시계열 데이터는 데이터의 분포(평균, 분산)의 변동성이 매우 큰 데이터이기 때문에 정규화 작업이 필수적이다. 대표적인 방법이 minmax, z-score 정규화인데 두 기법 모두 장단점을 가지고 있다. 일반적으로 z-score 정규화를 사용하게 되는데, 특히 z-score 정규화는 multi-modal 한 데이터에 취약하다는 단점이 있다. 이를 극복하기 위해 슬라이딩 윈도우를 도입해 윈도우 단위로 z-score 정규화를 적용하는 방법이 제안되었지만 마찬가지로 한계점(변동성의 차별성을 반영하지 못함) 이 존재한다. 해당 논문은 윈도우 단위의 정규화를 기본으로 하며 딥러닝 모델의 학습 성능을 높이는 방향으로 정규화에 사용할 통계(평균, 분산)을 end-to-end로 학습하겠다는 내용이다.

Algorithm

• Deep Adaptive Input Normalization (DAIN) 은 3가지 과정을 거쳐 데이터 정규화를 진행한다.
  • Adaptive Shifting
    해당 단계에서는 입력 데이터의 평균을 계산한다고 생각하면 된다. 입력 데이터의 실제 평균 ai 을 계산한 후에 해당 값을 MLP 에 입력하여 학습된 평균 αi 을 계산한다.

• Adaptive Scaling
  첫 번째 단계에서 평균을 구했으니까 여기서는 표준편차를 계산한다. 이전 단계에서 구한 학습된 평균 α 를 사용해서 일반적으로 표준편차를 계산하는 공식대로 편차 b 를 구한다. 그리고 마찬가지로 MLP 에 넣어서 학습된 편차 β 를 계산한다.

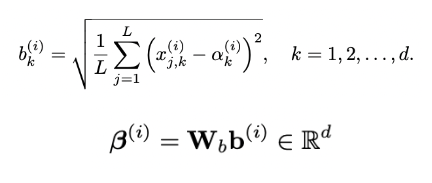
• Adaptive gating
  마지막 단계는 일종의 압축 단계라고 생각할 수 있다. 위의 2단계는 평균, 표준편차를 학습할 뿐 사실상 z-score 정규화와 틀은 다를 것이 없다. DAIN 은 마지막에 학습에 도움이 되는 feature 까지 분류할 수 있는 gating을 추가했다. 과정은 크게 어렵지 않은데, 위의 단계를 지나 정규화된 데이터에서 다시 평균 c 를 계산한 후에 MLP 에 넣어주어 γ 를 계산한다. 계산한 값을 정규화된 입력 데이터와 entrywise 하게 곱해주어 최종적으로 각 feature 별로 중요도가 곱해진 output을 얻게 된다.

Experiment

• 실험 결과는 DAIN 을 사용했을때 일반적으로 성능이 향상되었다고 한다. 아직 실험 결과는 자세히 보지 못했다. 
• 지금 진행하고 있는 연구에 적용해봤는데, 생각보다 괜찮은 성능을 보여주고 있다.

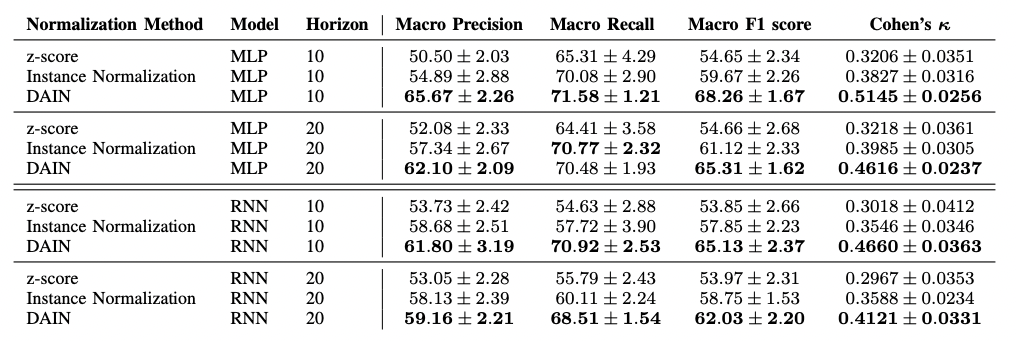
참고

소스 코드 링크 : https://github.com/passalis/dain