UNDERSTANDING DEEP LEARNING REQUIRES RETHINKING GENERALIZATION
논문 링크 : https://arxiv.org/pdf/1611.03530.pdf
1. Introduction
딥러닝은 왜 잘되는가? 라는 질문을 한번쯤은 들어봤을 것이다. 사실 이 질문은 현재까지도 완벽하게 해결되지 않은 질문이라고 생각되며 내가 딥러닝 공부를 시작하게 한 질문이며 연구주제이기도 했다. 딥러닝을 표현할때 흔히 블랙박스라는 단어를 많이 사용한다. 인간의 해석으로는 왜 딥러닝 모델이 그렇게 학습을 한 것인지, 무엇을 학습한 것인지 명확하게 설명하는 것이 사실상 불가능한 수준이기 때문이다. 그렇기 때문에 generalization, 즉 왜 일반화가 어제는 잘되고 또 오늘은 잘 안되는지 설명할 수가 없다는 것이다. 이를 위해서 representation learning 같은 주제로 많은 연구가 진행되고 있다. 해당 논문은 일반화의 성질에 대해 규명한 여러 이론 (VC-dimension, Rademacher complexity, Uniform stability) 등에 이의를 제기한 논문이다. (해당 이론들은 자세히 몰라서 추가로 리뷰할 예정...) 과장을 보태면 딥러닝 모델은 그 규모의 힘으로 그냥 데이터를 통채로 외운다는 것이다. 이를 증명하기 위해 여러 실험을 진행했고, 해당 논문은 아직도 우리는 딥러닝 모델의 일반화에 대해 이해하지 못했다는 것을 알려주고 있다.
2. Main
논문이 기여한 내용은 다음과 같다.
2.1 Randomization tests
저자는 간단한 CNN 모델을 사용해서 CIFAR10, ImageNet 에 대해 학습을 진행했는데 이때 학습 데이터의 라벨링을 완전히 랜덤하게 재부여했다. 그런데 놀랍게도 training error 가 0 이 되었다. 당연하게도 테스트 결과는 랜덤과 거의 유사한 수준이었지만 이는 놀라운 사실을 알려준다.

또한 이미지를 완전히 랜덤한 픽셀로 바꿔서 학습을 진행했는데 이때도 training error 는 0으로 수렴했다. CNN이 필터를 통해 이미지를 인식하는 구조임에도 랜덤 노이즈조차 학습이 가능하다는 것이다. 마지막으로 노이즈의 강도를 조절해서 원본 ~ 완전 노이즈 데이터에 대해 점차적으로 학습을 진행했다. 이때는 점차 일반화 에러가 증가하는 현상을 보여주었는데, 이는 CNN이 데이터에 남아있는 signal을 잡아낼 수 있으며 동시에 노이즈 조차도 학습이 가능하다는 사실을 보여준다.
2.2 The role of explicit regularization
모델 자체적으로 regularizer 의 성능이 부족하다면 우리는 추가적으로 regularizer를 사용한다. 여기서 저자는 explicit regularization 들이 정말 일반화에 도움이 되는가에 대해 아래와 같이 말했다.

일반적인 경우와 다르게 딥러닝에서는 regularization 이 다르게 역할을 한다는 것이다. 따라서 해당 regularization들이 일반화에 도움이 될 수는 있지만, 이것들을 제외한다고 해서 반드시 일반화 성능이 감소한다는 것은 아니라는 것이다. 심지어 한 논문에서는 l2-regularization이 오히려 최적화에 도움이 되었다고 하는데 이는 얼마나 우리가 딥러닝을 이해하지 못했는지 보여주는 사실이다.
2.3 Finite sample expressivity
해당 내용은 더 자세히 읽어봐야하는데 요약하면 일반적으로 큰 뉴럴넷은 학습 데이터의 어떠한 라벨링도 표현이 가능하다는 것이다. 2-layer ReLU 네트워크가 $2n + d$개의 파라미터를 가지고 있다면 해당 네트워크는 $n$개의 $d$차원 데이터를 표현할 수 있다고 한다. 기존의 논문들은 뉴럴넷이 표현할 수 있는 함수 자체에 관심을 두었다면 해당 논문은 데이터의 개수 관점에서 뉴럴넷의 표현력에 관심을 두었다고 한다.
2.4 The role of implicit regularization
위에서 explicit regularization 에 다루었다면 여기는 implicit regularization 에 대해 다룬다. 대표적인 implicit regularization이 SGD인데 linear model에서 SGD 는 항상 약간의 norm을 가진채로 solution에 수렴한다고 한다. SGD가 굉장한 역할을 하는 것은 분명하지만 논문 조차도 특정 모델이 다른 모델보다 일반화 성능이 좋은 이유는 아직 설명할 수 없으며 SGD에 대한 연구가 필요하다고 한다.
3. Result
3.1 FITTING RANDOM LABELS AND PIXELS
해당 논문은 feed-forward 뉴럴넷의 capacity를 효과적으로 탐구하는 것이 목적이다. 이를 위해 적당한 아키텍쳐를 선택한 후에 1) 정상 데이터 2) 랜덤하게 재라벨링한 데이터 에 대해 학습을 진행했다. 당연히 후자는 더 이상 데이터와 라벨링 사이에 연관성이 없기 때문에 학습이 불가능했어야한다. 하지만 놀랍게도 어떠한 조건에서도 뉴럴넷은 결국 학습 오차는 0으로 수렴하였다. 구체적인 실험 데이터는 아래와 같다.

위의 5가지 데이터에 대해 SGD 를 사용해서 학습한 결과 하이퍼 파라미터조차 바꾸지 않았는데 모두 완벽하게 학습이 가능했다. 아래의 그림은 실제로 학습을 진행한 결과를 나타낸 것이다.

(a)를 보면 데이터에 따라 약간의 차이는 있지만 결국 학습 오차가 0에 수렴하는 것을 알 수 있다. (b) 그림은 라벨링의 훼손 정도에 따라 수렴속도를 나타낸 것인데 마찬가지로 점차 시간이 소요되긴 하지만 어쨌든 수렴하게 된다. (c) 는 테스트 오차인데 학습 오차가 0 이기 때문에 일반화 오차와 같다고 봐도 무방하며, 여기서는 다행히도(?) 라벨링이 훼손될수록 일반화 성능은 낮아지는 것을 알 수 있다. 하지만 이는 학습이 잘된다면 일반화 오류도 낮을 것이라는 기존의 상식을 깨버리는 사실이다.
3.2 IMPLICATIONS
위의 결과를 통해 저자는 일반화에 대한 기존의 이론들에 이의를 제시했다.
3.2.1 Rademacher complexity and VC-dimension

Rademacher complexity는 어떤 가설에 대해 해당 가설이 얼만큼의 복잡성까지 수용할 수 있는지를 나타내는 지표라고 생각하면 된다. 여기서 $\sigma$ 는 반반확률로 -1, +1 의 값을 가지는 랜덤변수일때, 특정 가설이 위의 식을 최대화했을때 그 값을 rademacher complexity 라고 한다. 해당 문제에서는 $h(x_{i})$ 가 multi-classification 인 경우인데 논문에서는 그냥 binary-classification 이랑 비슷한 상황이니까 해당 문제를 고려해도 충분하다고 한다. 그런데 이때 complexity 를 최대화하려면 그냥 $\sigma$ 값이랑 반대가 되도록 학습하면 된다. 그러면 complexity는 어떤 가설을 대입해도 사실상 1에 가까운 수가 유지된다. 이때 문제가 발생하는데 아래의 식은 널리 알려진 머신러닝 모델의 generalization error 에 대한 수식이다. $E_{out}$ 이 테스트, $E_{in}$ 이 학습이라고 생각하면 된다. N은 데이터 수, M은 바로 model complexity 가 된다.

위의 식에서 빨간색 부분만 고려를 해서 간략하게 정리하면 아래와 같다.
$$E_{out} \leq E_{in} + \sqrt{{Complexity} \over{N}}$$
그런데 우리는 위애서 complexity 는 어떤 조건에서든 1에 매우 근사한 값으로 유지된다는 것을 알았다. 따라서 우변에서 2번째 항은 그대로이고 학습 에러($E_{in}$)는 0이니까 upper bound에는 변화가 없는 상태이다. 그런데 테스트 결과는 랜덤 라벨링을 적용함에 따라 매우 크게 달라진다. 따라서 해당 이론으로는 우리가 발견한 사실을 설명할 수가 없다는 것이다.
3.2.2 Uniform stability
Rademacher complexity가 가설에 대한 complexity를 설명했다면 이번엔 학습에 사용한 알고리즘을 고려해볼 차례이다. Uniform stability 는 특정 알고리즘이 데이터의 변화에 얼마나 민감한지를 나타내는 지표이다. 하지만 이것은 순수하게 알고리즘만을 고려한 지표로 라벨링의 분포, 데이터의 특성은 고려하지 않는다. 몇몇 논문에서 이것보다는 약한 의미의 stability를 제안하기는 했지만 여전히 해당 지표로 이 논문의 결과를 설명하기엔 무리가 있다.
4. THE ROLE OF REGULARIZATION
원래 regularizer의 역할은 특정 가설이 일반화를 잘하기엔 그 규모가 너무 클때 적당한 패널티를 부여함으로서 복잡성을 낮추는 것이다. 그런데 딥러닝에서는 explicit regularization 이 다르게 동작한다는 것이다. 실험에 의하면 dropout과 weight decay를 추가한 InceptionV3 모델이 완벽하지는 않더라도 랜덤 학습 데이터에 매우 잘 학습이 되었다고 한다. 또한 CIFAR10에서도 Inception, MLPs 모두 weight decay를 사용해도 랜덤 학습 데이터에 완벽하게 피팅이 되었다고 한다. 다만 AlexNet은 weight decay를 사용했을때 수렴하지 않았는데 이를 확인하기 위해 regularizers 을 추가 / 제외함에 따른 결과를 비교했다. 논문에서 사용한 regularizers 들은 아래와 같다.


실험결과 regularizer 들을 사용했을때 일반화 성능이 좋아지긴 했지만 사용하지 않는다고 해서 일반화성능이 아주 나빠지지도 않았다. 추가적인 실험 결과 data-augmentation이 weight decay, dropout 보다도 강력한 성능을 가지는 것 같다고 한다. 그 외에도 implicit regularization 에 대해서도 탐구한 결과 early stopping 이 일반화 성능을 높여줄 가능성이 있다고 했다. 다만 이에 대해서는 확실한 실험이 필요하다고 한다. Batch normalization 도 널리 알려진 implicit regularization인데 실험 결과 학습 곡선에 안정성을 주긴하지만 일반화 성능을 3~4% 정도의 차이밖에 없었다고 한다. 결과적으로 두 종류의 regularization 은 모두 적절히 사용한다면 일반화 성능을 높이는데에 도움이 될 수는 있지만 반드시 필요한 것은 아니라는 것이다.
5. FINITE-SAMPLE EXPRESSIVITY
위에서도 잠깐 언급했지만 해당 논문은 neural networks의 표현력을 데이터의 개수 관점에서 해석하는 것에 중점을 두었다. 여러 내용을 설명하고 있지만 그냥 결론만 말하자면
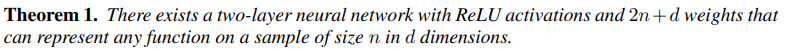
이에 대한 증명은 appendix 에 있는데 천천히 따라가면 크게 어려운 내용은 아니었다.
6. IMPLICIT REGULARIZATION: AN APPEAL TO LINEAR MODELS
해당 내용은 확실히 이해한 것인지 모르겠다. 해당 세션에서는 간단한 선형 모델을 예시로 뉴럴넷에 대한 이해도를 높이고자 했다. 우리가 d-차원으로 구성된 n 개의 ${(x_{i}, y_{i})}$ 데이터 쌍을 가지고 있다고 가정하자. 그때 단순한 모델의 목적함수를 구성하면(정확히는 empirical risk minimization (ERM) )

이때 $d \geq n$ 이라면 모든 라벨링에 대해서 피팅이 가능하다. 그렇다면 이러한 모델을 explicit regularization 없이도 일반화를 잘할 수 있을까? $X$를 $n \times d$ 의 행렬이라고 가정해보자. 그리고 $X$ 가 rank n 이라면 $Xw = y$ 는 무한한 답을 가지게 되고 단순히 이 식을 품으로써 global minimum 을 찾을 수 있다. 그런데 모든 global minimum이 다 일반화를 잘할까? 이를 수치적으로 평가하기 위해 loss function의 curvature 를 사용했지만 모든 optimal solution 에서 해당 값이 같다는 것이 증명되었다. 그렇다면 다른 지표는 무엇이 있을까? 이때 제안된 것이 SGD 이다. SGD가 weight를 학습해가는 과정을 식으로 표현하면 $w_{t+1} = w_{t} - \mu_{t}e_{t}x_{i_{t}}$ 로 나타낼 수 있다. 이때 $w_{0}=0$ 이라는 특수한 상황에서 전체 과정은 $w = \sum_{i=1}^{n}\alpha_{i}x_{i} = X^{t}\alpha$ 로 볼 수 있다. 우리가 해결하고자 하는 $Xw = y$ 는 다시 표현하면
$$XX^{T}\alpha = y$$
로 표현이 가능하고 이때는 unique solution 만이 존재한다. $XX^{T}$가 invertible 이기 때문이라고 생각했는데, 몇분은 아니라고 설명하신다...뭘까... 이때 $K = XX^{T}$라고 생각한다면 위의 수식은 일종의 kernel trick 에 해당한다. 따라서 $K\alpha = y$를 푸는 것으로 우리는 최적의 솔루션을 찾을 수 있는데, 여기서 또 다시 놀라운 점은 이것이 minimum-norm solution을 찾는 것과 동일한 형태라는 것이다. 즉, SGD 로 솔루션을 찾아가는 것 자체가 minimum-norm solution을 적용하는 것과도 마찬가지라는 것이며 l2-norm 의 크기가 뉴럴넷의 성능 평가의 지표로 활용될 수도 있다는 것이다. 실제 실험 결과도 CNN에 l2-regularization 을 적용했더니 테스트 에러가 2% 정도 감소했다고 한다. 그리고 랜덤 라벨에 학습한 모델의 norm을 살펴본 결과 그 값이 minimum-norm solution 과 비교해 매우 크다는 것도 확인했다.
그런데 아쉽게도 l2-norm은 일반화 성능 지표로 사용할 수 없다. MNIST 실험에서 minimum-norm solution에서 l2-norm 은 대략 220, 테스트 에러는 1.2% 였다. 그런데 wavelet preprocessing을 거친 후에는 l2-norm은 390으로 증가했지만 오히려 에러는 0.6% 로 감소하였다. 따라서 SGD가 minimum-norm solution 과 유사하다는 것은 맞지만 일반화를 완벽히 설명하는 것은 여전히 불가능하다는 것이다.
참고자료
https://becominghuman.ai/machine-learning-and-generalization-error-vc-bound-in-practice-7ff80a85c1db
https://nanohub.org/resources/32763/watch?resid=33448.
http://web.eecs.umich.edu/~cscott/past_courses/eecs598w14/notes/10_rademacher.pdf