Mokssi's repository

1. Introduction

논문 링크 : http://proceedings.mlr.press/v80/ruff18a/ruff18a.pdf

해당 논문은 Anomaly Detection 분야에서 베이스라인으로 자리잡은 DeepSVDD 라는 모델이다. 근간이 되는 이론은 SVM(정확히는 OC-SVM) 과 매우 유사하다. OC-SVM latent space 에서 정상 / 비정상 클래스를 구분할 수 있는 가상의 hyperplane 을 찾아내는 문제였다면, SVDD 는 어떤 중심점을 기준으로 가상의 원을 찾아내겠다는 이론이다. 그리고 이를 딥러닝에게 맡기겠다는 것이 DeepSVDD 이다.  OC-SVM 도 좋은 알고리즘이지만 고차원 데이터에서는 잘 작동하지 않기 때문에 이러한 방법이 제안되었다.

2. Background

2.1 Kernel-based One-Class Classification

SVM 이론은 깊숙히 들어가면 굉장히 어려운 이론이기 때문에 공식으로만 이해한다면

첫번째 term 은 일종의 보정(regularizer)이라고 생각하면 된다. 두번째 term은 원점과 hyperplane 까지의 거리로 목적함수에 의하면 최대한 값이 커지게 하는 것이 목적이다. OC-SVM은 무조건 원점을 기준으로 정상 / 비정상 클래스를 나누기 때문에 원점으로부터 hyperplane을 최대한 멀어지게 하는 것이 바람직하다는 말이다. 마지막 term 은 매핑된 데이터들과 hyperplane 까지의 거리를 의미하며 $v$ 값은 trade-off 값이다. 해당 term 은 논문에서 slack variables 라고 부르는데 해당 변수를 통해 soft / hard boundary 를 조절할 수 있다. 위의 목적함수에 따라 최대한 많은 데이터 포인트가 hyperplane 바깥에 위치하게 된다.

2.2  SVDD

SVDD 도 마찬가지로 공식만 살펴본다면

R 은 경계면까지의 반지름을 의미하며 마찬가지로 soft / hard boundary 를 결정하는 변수도 있다. 

3. Main

3.1 Deep SVDD

원리는 위에서 설명한 SVDD 와 동일하다. 다만 OC-SVM, SVDD 는 원하는 hyperplace, sphere 를 계산하기 위해서 복잡한 과정(라그랑주)을 거쳐야한다. 이것을 딥러닝으로 해결해보자는 접근법이 Deep SVDD 이다. Deep SVDD 의 목적함수는 아래와 같다.

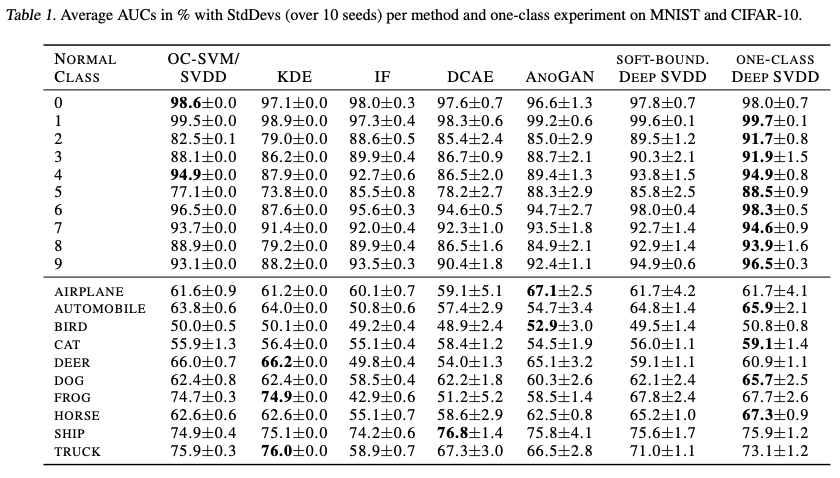
마찬가지로 반지름은 최대한 줄이면서, 동시에 원 밖에 있는 데이터들도 경계면에 최대한 근접하게 하는 것이 목적이다. 거기에 약간의 regularization 을 추가하면 최종목적함수가 된다. 논문에서 제시한 기본 모델은 위의 목적함수에 따라 학습을 진행하며 이를 SOFT-BOUND. Deep SVDD 라고 명명했다. 여기에 추가로 간단한 버전의 모델도 제시했으며, 해당 모델의 목적함수는 아래와 같다. (결과적으로는 후자모델이 더 성능이 좋았다.)

원 밖의 데이터들의 경계면까지의 거리는 더 이상 고려하지 않고, 그냥 모든 데이터에 대해서 중심점까지의 거리를 최대한 줄여주겠다는 뜻이 된다. 단순히 모든 데이터들의 평균거리를 고려함으로서 SOFT-BOUND. Deep SVDD 와 비슷한 효과를 기대한다고 한다. 다만 이를 위해서 학습 데이터의 상당수는 한 개의 클래스에서 추출되었다고 가정했다. 

3.2 Properties of Deep SVDD

저자는 Deep SVDD 의 학습이 제대로 이루어지려면 4가지 특성을 충족해야 한다고 설명했다.

3.1.1 All-zero-weights solution

명확히 이해한 것인지는 모르겠지만 간략히 설명한다면 중심점이 제대로 설정이 되지 않는다면 뉴럴넷의 모든 weight이 0이 되는 결과를 얻을 수 있다는 것이다. 모든 값이 0인 weight 를 $W_{0}$ 라고 한다면 이 뉴럴넷은 모든 입력을 한 점 $c_{0}$으로 매핑할 것이다. 그런데 만약 우리가 최적화할 중심 $c$를 $c_{0}$ 로 설정한다면 뉴럴넷은 진짜로 $W_{0}$ 로 학습이 될 것이다. 따라서 적절한 중심점을 선택하는 것이 매우 중요하며 논문에서는 실험결과 학습 데이터 일부를 forward 시킨 다음에 평균을 구하는 것이 괜찮다고 한다.

3.1.2 Bias terms

이것도 이전 경우와 약간 비슷한 경우인데, 특정 layer 에서 만약 weight 값들이 모두 0이라면 어떤 입력이든 결국 bias term 에 의해 다음 layer 로의 input 이 결정된다. 이럴 경우 뉴럴넷이 그냥 어떤 입력이든 $c$로 매핑하는 bias 를 학습할 가능성이 있다는 것이다. 따라서 Deep SVDD 에서는 모든 레이어에서 bias 를 사용하지 않았다.

3.1.3 Bounded activation functions

해당 특성은 bouned activation function 을 사용할 경우 발생할 수 있는 특성에 대한 설명이다. 만약 우리가 가진 데이터 중에서 특정 차원의 데이터가 모두 양수라고 가정해보자. 그런데 이때 bounded activation function(sigmoid, tanh) 를 사용하게 된다면 한 쪽 방향으로만 계속 이동하게 될테고 결국 포화상태에 이르게 된다. 즉, 모든 입력에 대해서 해당 dimension 의 weight 는 그냥 무작정 크게 학습이 된다는 것이다. 그렇게 학습을 해도 bounded 이기 때문에 최대값은 커질 수 없기 때문이다. 그렇게 된다면 이후에는 또 다시 bias term 들에 의해 입력에 상관없이 똑같은 output을 내는 네트워크가 완성될 가능성이 생기게 된다. 따라서 그냥 ReLU 를 쓰라는 것이다.

3.1.4 ν-property

이것은 SOFT-BOUND 버전 모델에 적용되는 사항으로 일단은 넘어가도록 하겠다.

4. Experiment

연구를 하다보면 정말 많은 논문을 읽게 되는데 보통 새로운 분야의 논문을 읽을때 서베이 논문부터 읽어보고 대충 흐름을 파악하고는 한다. 그러다보면 근원이 되는 논문, SOTA 논문 등을 자연스럽게 알게 되고 하나하나 읽어보면서 레퍼런스를 계속해서 추적하게 된다. 근데 그 과정에서 논문을 혼동하는 일이 많이 발생했다. 레퍼런스도 양식이 다양하고 논문 본문에서는 해당 레퍼런스가 어떤 논문인지 정확히 파악할 수가 없어서 내가 이 논문을 읽어봤었는지도 헷갈린다. 또한 같은 주제로도 워낙 다양한 논문이 많다보니까 어떤 논문에서는 서브 주제로 a 논문을 추천하고, 어떤 논문에서는 같은 서브 주제로 b 논문을 추천하고... 그러다보니 어떤 걸 읽어야하는지 너무 혼동이 되서 내가 읽은 논문들이 인용한 논문들을 리스트로 모두 뽑아낼 수 있다면 통계를 내서 상위 논문부터 읽으면 편하지 않을까? 하는 생각을 하게 되었다.

그런데 이것이 생각보다 어려운 일인지 구글에 검색을 해도 내가 원하는 프로그램을 찾을 수가 없었다... google scholar, 아카이브 등에서 레퍼런스를 추출해가는 것에 굉장히 민감한? 모양이다. 그래서 pdf 에서 직접 추출할 수 밖에 없는데 이것이 생각보다 까다로운 일이었다. 해당 주제로 또 다른 논문이 있을 수준...

결국 python 라이브러리에서 레퍼런스를 리스트로 추출할 수 있는 라이브러리를 발견해서 사용해보았는데, 텍스트 기반으로 추출하는 것인지 정확하지는 않았다. 그래도 이것이 어디냐는 마음으로 유용하게 사용해보겠다...

라이브러리 소개

사용결과

전체 텍스트(raw ref), 제목(misc), 연도(year) 의 딕셔너리로 레퍼런스를 추출해준다. 정확도가 높은 편은 아니지만 쓸만한 것 같다. 사용하기 전에 libmagic 관련 에러가 높은 확률로 나올텐데 아래 3가지 방법으로 에러가 해결된다. 알아본 바로는 magic이라는 프로그램 자체가 리눅스 환경에서 python 사용을 쉽게하기 위한 모듈인데, 윈도우 용으로 수정된 모듈이 python-magic-bin 이라고 한다. 추가로 맥에서도 사용해본 결과 맥에서는 사용이 불가능한 것 같다. 메모리 관련 에러가 나오는데 아마 수정이 불가능한 문제인 것 같다. 윈도우에서만 사용하자.

!pip install magic
!pip install libmagic
!pip install python-magic-bin

그 외의 방법

Scholarcy Reference Extraction API

Scholarcy 라는 단체에서 만든 API 인데 refextract 라이브러리와 비슷하게 동작한다. 다양한 형태의 입력, 출력을 지원하기 때문에 해당 API를 사용해도 괜찮아보인다. 화면 구성은 bentoML로 보인다.

1. Introduction

인과관계추론(causal inference)는 예전부터 해결하기 어려운 문제이고, 다양한 분야로 활용이 가능하다. 해당 논문은 2018년에 발표된 논문으로 graph neural network와 variational autoencoder 를 함께 사용해서 다이나믹 시스템의 인과관계를 추론 및 각 노드들의 미래를 예측하는 모델이다. 대학원생때 잠깐 공부했던 분야라 현재 트랜드는 잘 모르지만 발표 다시부터 지금까지 굉장히 많은 주목을 받은 논문인 것은 확실하다. 지금은 해당 모델도 한계점이 많이 발견되서 다양한 변형들이 많이 나오고 있다고 한다. 확률공부하다가 생각나서 다시 개념환기도 시킬 겸 리뷰를 작성해보았다.

2. Background

2.1 Causal inference

인과관계(causality)는 사실상 우리 주변에서 발생하는 모든 것들에 작용하고 있다. 우리가 팔을 움직을때, 걷기 위해 발을 움직일때 모두 관절들 사이의 인과 관계라고 볼 수도 있다. 학생들의 시험 성적을 공부시간, 공부량 등으로 모델링한다면 어느 정도의 인과관계가 존재할 것이다. 물론 공부시간이 많다고 무조건 성적이 좋은 것은 아니지만...
이렇게 인과관계를 명확히 파악할 수 있다면 다양한 활용(주식 예측 등)이 가능하다. 하지만 이것을 힘들게 하는 요인이 있는데 바로 association 이라는 것이다. 간단하게 설명하면 직접적인 영향이 causality 라면 간접적인 영향이 association 이다. 우리가 어떤 시스템을 관찰할때 X, Y라는 변수가 서로 직접적인 영향을 주고 받는다고 생각했지만, 알고보니 Z 라는 숨은 변수가 실제 원인이었던 것이다. 이럴때 X, Y는 서로 causality가 아니라 association 의 관계가 형성된다. 하지만 우리는 그것을 causality 라고 잘못해석하고 프로젝트를 진행하는 것이다. 그래서 이러한 요소를 잘 잡아내는 것이 매우 중요하다.

2.2 Graph neural network

그래프 형태의 데이터를 다루기 위한 뉴럴 네트워크이다. 서로 상호작용하는 여러 엔티티가 존재하는 시스템은 그래프로의 해석이 매우 적절한데 해당 논문도 이를 활용했다. 노드들간의 작용하는 어떠한 힘을 메시지로 모델링함으로써 효율적으로 인과관계를 예측할 수 있다.

3. Main

3.1 Encoder

모델은 전형적인 GNN의 형태를 가져왔다. Encoder에서는 각 노드들의 time step 입력을 받아서 최종적으로는 엣지 타입에 대한 hidden state($z_{ij}$)를 찾아낸다. 각 노드들의 hidden state $h_{i}^{l}$ 을 사용해서 source, destination 의 순서에 맞게 MLP($f_{e}^{l}$) 에 입력하여 엣지의 hidden state를 계산한다. 그리고 하나의 노드를 기준으로 해당 노드에 들어오는 엣지들의 hidden state를 aggregation(여기서는 sum)하여 노드의 hidden state를 업데이트한다. 이후는 미리 정해둔 업데이트 수만큼 반복된다. 최종적으로 업데이트된 엣지 hidden state에 softmax를 취해주면서 edge type를 모델링하게 된다. 

3.2 Sampling

이전 단계에서 각 엣지들의 hidden state 에 softmax를 취해서 엣지 타입을 얻어낸다고 했다. 이것은 variational autoencoder의 자연스러운 흐름 중에 하나인데 이때 gradient 계산을 위해 reparamerization trick을 사용하게 된다. 간단하게 말하면 softmax 라는 행동을 통해 우리는 일종의 sampling을 하게 된 것인데 이 행동 자체가 미분이 불가능한 행동이다. 그런데 우리는 뉴럴 네트워크를 grdient를 통해 학습하기 때문에 미분을 해야만한다. 그래서 sampling 을 통해 얻어낸 변수(여기서는 z)를 일종의 함수로 변형하여 미분 가능하게 변형하는 것을 reparamerization trick 이라고 한다. 그런데 해당 모델은 여기서 더 나아가 z 라는 것이 엣지의 타입이기 때문에 discrete 한 변수이다. 예를 들어 softmax를 통해 [0.7, 0.3] 이라는 분포를 얻었고, z를 sampling 했더니 [1, 0] 이라는 엣지 타입을 얻었다. 하지만 이것이 미분이 불가능하다는 것이다. 따라서 한가지 장치가 더 적용되는데 gumbel softmax라는 함수이다. gumbel softmax는 softmax의 변형인데, 강도를 조절할 수 있는 softmax라고 생각하면 된다.

3.3 Decoder

Decoder에서는 이전 단계에서 얻은 $z_{ij}$, 각 노드들의 입력($x_{i}^{t}$) 들을 사용해서 각 노드들의 다음 스텝을 예측한다. 이때 정확한 좌표값을 예측하는 것이 아니라 대략적인 위치 예측을 위한 평균, 분산을 계산한다. 모델 자체는 그렇게 특별한 것은 없다. 모델 최적화를 위해 해당 모델은 한가지 추가적인 장치를 적용했다. 해당 모델은 기본적으로 one-step prediction을 수행한다. 즉, 한번에 한번의 미래만 예측한다는 것이다. 이러한 방법을 선택했을때 발생할 수 있는 문제점은 너무 짧은 인과관계만 반영이 된다는 것이다. 이를 예방하기 위해 NRI는 2가지 전략을 선택했다. 첫번째는 multiple-step을 예측한다는 것이다. 두번째는 엣지 타입별로 다른 MLP를 적용한다는 것이다. 위의 수식에서 첫 번째 수식의 MLP가 엣지 타입 ($k$) 에 따라 다르게 적용된 것을 알 수 있다. 아래의 수식은 multiple-step 을 어떻게 구현했는지 설명한다. M step 마다 정답을 주고 그 사이에는 예측된 평균을 사용해서 다시 평균을 예측하는 방식이다.

리뷰 논문: Deep Adaptive Input Normalization for Time Series Forecasting
https://arxiv.org/abs/1902.07892

Introduction

딥러닝에서 데이터 전처리는 필수적인 단계이다. 아웃라이어, 측정오류 등 사전에 데이터를 가공하지 않으면 성능에 큰 문제가 발생할 수 있기 때문이다. 그 중에서 데이터의 분포, modality 로 인해 딥러닝의 성능이 좌우되는 경우가 많다. uni-modal 한 환경이라면 큰 문제가 되지 않지만, real data 들은 multi-modal 한 경우가 대부분이기 때문에 이를 위한 전처리가 필수다. 특히 시계열 데이터는 데이터의 분포(평균, 분산)의 변동성이 매우 큰 데이터이기 때문에 정규화 작업이 필수적이다. 대표적인 방법이 minmax, z-score 정규화인데 두 기법 모두 장단점을 가지고 있다. 일반적으로 z-score 정규화를 사용하게 되는데, 특히 z-score 정규화는 multi-modal 한 데이터에 취약하다는 단점이 있다. 이를 극복하기 위해 슬라이딩 윈도우를 도입해 윈도우 단위로 z-score 정규화를 적용하는 방법이 제안되었지만 마찬가지로 한계점(변동성의 차별성을 반영하지 못함) 이 존재한다. 해당 논문은 윈도우 단위의 정규화를 기본으로 하며 딥러닝 모델의 학습 성능을 높이는 방향으로 정규화에 사용할 통계(평균, 분산)을 end-to-end로 학습하겠다는 내용이다.

Algorithm

• Deep Adaptive Input Normalization (DAIN) 은 3가지 과정을 거쳐 데이터 정규화를 진행한다.
  • Adaptive Shifting
    해당 단계에서는 입력 데이터의 평균을 계산한다고 생각하면 된다. 입력 데이터의 실제 평균 ai 을 계산한 후에 해당 값을 MLP 에 입력하여 학습된 평균 αi 을 계산한다.

• Adaptive Scaling
  첫 번째 단계에서 평균을 구했으니까 여기서는 표준편차를 계산한다. 이전 단계에서 구한 학습된 평균 α 를 사용해서 일반적으로 표준편차를 계산하는 공식대로 편차 b 를 구한다. 그리고 마찬가지로 MLP 에 넣어서 학습된 편차 β 를 계산한다.

• Adaptive gating
  마지막 단계는 일종의 압축 단계라고 생각할 수 있다. 위의 2단계는 평균, 표준편차를 학습할 뿐 사실상 z-score 정규화와 틀은 다를 것이 없다. DAIN 은 마지막에 학습에 도움이 되는 feature 까지 분류할 수 있는 gating을 추가했다. 과정은 크게 어렵지 않은데, 위의 단계를 지나 정규화된 데이터에서 다시 평균 c 를 계산한 후에 MLP 에 넣어주어 γ 를 계산한다. 계산한 값을 정규화된 입력 데이터와 entrywise 하게 곱해주어 최종적으로 각 feature 별로 중요도가 곱해진 output을 얻게 된다.

Experiment

• 실험 결과는 DAIN 을 사용했을때 일반적으로 성능이 향상되었다고 한다. 아직 실험 결과는 자세히 보지 못했다. 
• 지금 진행하고 있는 연구에 적용해봤는데, 생각보다 괜찮은 성능을 보여주고 있다.

참고

소스 코드 링크 : https://github.com/passalis/dain

원본 논문: https://www.cs.toronto.edu/~vmnih/docs/dqn.pdf

• 강화학습을 DNN에 적용한 최초의 논문

강화학습이란 ?

• 현재 머신러닝은 크게 3가지로 분류된다.
  1. 비지도 학습(Unsupervised learning)
  2. 지도 학습(Supervised learning)
  3. 강화 학습(Reinforcement learning)

강화학습도 비지도학습의 일부가 아니냐는 주변분들의 의견이 있긴하지만 
크게 3가지로 나누는 것에 이견은 없는 것으로 보인다.

• 강화학습은 쉽게 표현하면 연속적인 결정 을 내리는 과정이라고 볼 수 있다. 그리고 그 결정은 순수하게 보상이라는 것에 의해 결정된다.
• 강화학습에는 행동의 주체 에이전트(agent), 행동(action), 보상(reward), 환경(environment) 가 존재한다.
• 정책(policy), 가치함수(value function) 등 더 세부적인 내용이 있지만 결국 설계자가 지정한 보상을 최대로 하는 행동을 알아내고 수행하는 것이 강화학습의 작동원리이다.

• 정책(policy), 가치함수(value function) 등 더 세부적인 내용이 있지만 결국 설계자가 지정한 보상을 최대로 하는 행동을 알아내고 수행하는 것이 강화학습의 작동원리이다.

2022 ICLR spotlight 논문 ANOMALY TRANSFORMER 리뷰 https://arxiv.org/pdf/2110.02642.pdf

참고사항

Reconsturction-based anomaly detection

• 비지도 학습 anomaly detection 의 하나로 가장 많이 사용되는 방법 중 하나
• 시계열 데이터를 입력받아 latent space(잠재 공간)을 만들어 입력 데이터를 그대로 복원시키는 방법
• 이때 원본 데이터와의 차이(에러)를 기준으로 정상 / 비정상 데이터를 구분
• PCA, AE, VAE 등이 대표적인 알고리즘
• AE, VAE 에서는 뉴럴넷을 사용해 잠재 공간을 형성해주는데 이때 시계열 데이터의 연관성을 학습하기 위해 RNN, LSTM, GRU을 적용한 사례가 많습니다. 해당 모델은 트랜스포머를 사용하여 연관성을 학습한 모델입니다.

Anomaly

• Point
  • Global outliers
    • 다른 포인트들과 확연히 다른 데이터 포인트. 주로 스파이크 데이터를 말합니다.
  • Contextual outliers
    • 주어진 context(흐름) 상에서 벗어난 데이터로 주로 이웃한 데이터 포인트에 대해 정의됩니다. 배열 데이터에서 작은 glitches 등이 있습니다.
• Pattern
  • Shapelet outliers
    • shapelet은 "분류 성능 향상에 가장 크게 도움이 되는 부분 시계열" 이라고 정의할 수 있습니다.
    • shapelet outliers는 기저가 되는 shaplet에서 벗어난 부분 시계열을 말합니다.
  • Seasonal outliers
    • 시계열 전반적인 seasonality(계절성)에서 벗어난 부분 시계열
    • 기저 shaplet 과는 유사하지만 계절성이 다른 데이터
  • Trend outliers
    • 데이터의 평균을 영구적으로 바꾸는 등 시계열 데이터의 트랜드를 크게 바꿔놓는 부분 시계열
    • 정상적인 기저 shaplet, seasonality 를 모두 가지고 있지만 트랜드를 바꾸는 경사가 매우 급한 데이터

1. Summary

• Key word : Anomaly transformer, association Discrepancy, minimax strategy
• Anomaly Transformer
  • 기존의 트랜스포머 모델을 사용하여 시계열 데이터 내에서 포인트들간의 연관성을 학습할 수 있도록 변형
• Association Discrepancy
  • 어노말 트랜스포머는 시계열 데이터 내에서 prior-association, series-association 이라는 2가지 연관성을 학습합니다.
    • Prior-association(P) : 인접한 데이터들간의 연관성, 시간 차이를 기준으로 가우시안 분포로 모델링하기 때문에 prior이라는 단어를 사용했습니다.
    • Series-association(S) : 시계열 전체에서 데이터들간의 연관성, self-attention에 의해 모델링
  • 2가지 분포의 차이(distance)를 association discrepancy(이하 AssDis)라고 부르며, 어노말 트랜스포머는 2개의 값을 교차로 최적화시켜 결과적으로 이상/정상 데이터의 AssDis이 구분되도록 하는 것입니다.
  • 저자는 이상 데이터는 오직 인접한 데이터와 연관성이 높게 나타나지만, 정상 데이터라면 시계열 전체에 걸쳐 연관성이 나타날 것이라고 주장했습니다. 따라서 이상 데이터라면 P, S 분포가 모두 인접 데이터에 밀집하게 되며 AssDis 가 작아지게 됩니다.

2. 본문

• 입력 데이터 : (d 차원으로 구성된 N개의 time step)

$$ \mathcal{X} = \{ x_{1}, x_{2}, ... , x_{N} \} \\ x_{t} \in \mathbb{R}^d $$

• 모델 구조
  • Anomaly Attention, Feed Forward 2개의 블록이 하나의 인코더를 구성하며 L 개의 인코더를 쌓아올리는 구조

2.1 Anomaly Attention

• 입력 데이터 : x (time series)
• 출력 데이터 : z (hidden state)
• 입력 데이터를 받아서 prior, series association, hidden state를 계산하는 블록

• Query, Key, Value는 모두 같은 input time series로부터 생성(self-attention) 하며 추가로 prior-association에서 사용할 표준편차(sigma)도 학습으로 생성
• Prior-Association은 가우시안 분포로 계산하며 row sum 나눠주는 rescale을 수행합니다.
• 실제로 학습된 모델에서의 sigma
  • Anomaly point 에서는 sigma가 급격히 감소하는데 이는 비정상 데이터가 인접한 데이터와 유사성이 강하게 나타나기 때문에 분산이 매우 작게 학습되는 것으로 해석할 수 있습니다.

• 추가적으로 가우시안 분포가 아닌 power-law 분포로 모델링했을 경우도 대체로 좋은 성능을 보여주었지만 가우시안 분포가 최적화가 더 쉽기 때문에 더 좋은 성능을 보였습니다.

2.2 Feed Forward

• 입력 데이터 : z (hidden state)
• 출력 데이터 : x (reconstruction time series)
• anomaly attention 블록의 출력(hidden state)를 입력받아 입력 데이터(x)를 재현하는 블록

2.3 Association Discrepancy

• KL-divergence 를 사용하여 prior, series association 분포의 차이를 계산했으며 위의 식은 Symmetrized Kullback–Leibler Divergence 이라고 불리는 distance 측정 방법입니다.
  • 그 외에도 4가지 distance(Jensen-Shannon Divergence, Wasserstein, Cross-Entropy, L2)를 사용하여 AssDis를 계산했는데 위의 수식이 가장 좋은 성능을 보여주었습니다.

• 한 번의 layer(L)가 끝나면 prior, series 는 (batch, header, N, N)의 분포를 가진 확률값을 가집니다.
• 이를 사용해 우선 time step 기준 (batch, header, N) 크기의 KL-divergence를 계산한 후에 header 기준 평균(batch, N)을 계산합니다. 그리고 마지막으로 batch * N 개의 평균을 계산합니다.
• 이러한 값이 총 L 개가 KL-divergence 값이 쌓이게 되며 이 값의 평균이 최종 AssDis 값이 됩니다.
• 단일 layer만을 사용하는 것보다 여러 layer의 평균을 사용할 경우 더 좋은 성능을 얻을 수 있었습니다.

2.4 Minimax Association Learning

• 모델에서 사용된 최종 손실 함수 reconstruction 차이와 AssDis를 결합하여 사용했습니다.

• 람다의 부호는 AssDis의 크기를 조절해주는 역할을 합니다.
  • Maximize Phase(람다 > 0)
    • Maximize 단계에서는 AssDis 값이 커지도록 최적화가 진행됩니다.
    • 이때 prior-association은 고정하며 series-association 만 조절하여 특정 time point가 인접하지 않은 time point들과의 연관성을 높이도록 학습합니다.
  • Minimize Phase(람다 < 0)
    • Minimize 단계에서는 AssDis 값이 작아지도록 학습합니다.
    • 반대로 series-association은 고정하며 prior-association이 series-association에 유사해지도록 학습이 진행됩니다.
• prior-ass 이 series-ass 에 근접하도록 학습하며 series-ass는 이와 반대로 학습이 진행되기 때문에 학습이 진행될수록 인접하지 않은 time point들과의 연관성에도 주목하도록 모델이 학습됩니다. 이때 reconstruction 에러와 함께 학습이 진행되기 때문에 비정상 데이터는 위의 내용을 학습하는 것이 정상 데이터에 비해 어렵다는 것이 anomaly transformer의 주요 내용입니다.

2.5 Anomaly Score

• Anomaly score는 위에서 계산한 AssDis와 복원한 입력(x)를 사용하여 point-wise 하게 계산합니다.

• 비정상 데이터라면 AssDis가 작게 나타나기 때문에 anomaly score은 크게 나타납니다.
• anomaly score가 threshold 보다 크다면 비정상 데이터로 판별됩니다. 성능 평가 단계에서는 비정상 구간 내에서 한 포인트라도 비정상이 감지된다면 해당 비정상 구간은 모두 탐지가 되었다고 간주합니다.
• threshold는 데이터 분포를 조사한 결과 anomaly score를 계산한 후 데이터 개수를 기준으로 비율로 계산합니다. (SMD는 0.5 %)
• 실제코드와 논문과의 차이점 : Test 단계에서 AssDis를 계산할때 layer의 평균이 아닌 layer단위로 KL-divergence에 temperature(오픈소스에서는 50) 곱한 후 sum을 해주었는데 해당 내용은 논문에서 자세한 설명을 찾지 못했습니다. 값의 단위가 커졌을 뿐 큰 틀은 변하지 않아서 크게 영향을 줄 것 같지는 않고 softmax 때문에 추가된 것으로 생각됩니다.

$$ AssDis(\mathcal{P, S;X}) = temperature \times \sum_{l=1}^{L}{(KL(P^{l}{i,:} ||S^{l}{i,:}) + KL(S^{l}{i,:}|P^{l}{i,:}))}_{i=1,...,N} \\ temperature = 50 $$

• 그 외에도 3가지 다른 anomaly score 측정 방법을 적용한 결과 Recon, AssDis 을 곱해서 사용한 위의 경우가 가장 좋은 성능을 보여주었습니다.

3. Experiments

• 데이터셋
  • SMD, MSL, SMPA, SWaT, NeurIPS-TS
• 주요 하이퍼 파라미터
  • 슬라이딩 윈도우 = 100(SMD는 50)
  • r = 0.1% for SWaT, 0.5% for SMD and 1% for other datasets
  • model dimension = 512
  • Encoder Layer = 3
  • head = 8
  • 람다 = 3
  • learning rate = 0.0001
  • 10 epochs, 32 batch size

3.1 5 real dataset 결과

3.2 Ablation study

• 총 3가지 block에 대해 ablation study를 진행

Anomaly Criterion

• Recon
• AssDis
• Assoc

Prior-Association

• Learnable
• Fix

Optimization Stragtegy

• Minimax
• Max

• AssDis 를 사용하는 것이 더 좋은 성능을 보여주었고, recon까지 결합하는 것이 최상의 효과를 보여주었습니다.
• Prior-association의 분산을 학습시키는 것이 더 좋은 성능을 보여주었으며, series-association만을 학습(maximize)보다는 prior 도 같이 학습하는 것이 최적의 성능을 보여주었습니다.

3.3 Recon vs. Assoc

• NeurIPS-TS에 있는 다양한 패턴의 시계열 데이터를 사용해 왜 어노말 트랜스포머가 잘 작동하는지 보다 직관적으로 해석했습니다.
• 아래의 그림에 의하면 많은 anomaly detection 에서 사용하는 reconstruction criterion과 비교해 association-based criterion의 경우 정상/비정상 데이터의 anomaly score가 보다 명확하게 구분되고 있습니다.

3.4 Prior-association

• 어노말 트랜스포머는 minimax 최적화 전략을 선택했는데 이 과정에서 prior-association은 series-association과 유사해지도록 학습됩니다. 따라서 분산을 학습시키는 행동이 prior-assocation가 인접 데이터에 얼마나 주목하는 정도를 조절할 수 있습니다.

3.5 Minimax strategy

• Maximize 단계에서 series-association은 prior-association에 멀어지도록 학습하기 때문에 결과적으로 인접하지 않은 데이터에 더욱 주목하도록 학습됩니다.
• 이때, 더 좋은 성능을 얻으려면 비정상 데이터는 정상 데이터보다 인접 데이터에 대한 주목도가 더 높아야 합니다. 하지만 단순히 maximize 만을 사용한다면 이러한 효과를 보기 어려우며 minimax 전략을 사용해야만 series-association에 강력한 제약이 적용됩니다.
• 아래의 표는 recon, max, assoc 전략을 사용했을때 정상/비정상 데이터 간의 구분 정도(인접 데이터와의 association weight)를 나타내며 abnormal/normal 값이 클수록 두 데이터가 명확하게 구분됨을 의미합니다.

3.6 Threshold Selection

• 논문에서는 Gap Statistic method 라는 데이터 내의 cluster의 개수를 결정하는 방법을 사용하여 threshold를 선정했습니다.
• 결과적으로 각 데이터셋의 anomaly score는 3개의 cluster로 나눠지며 이를 기준으로 threshold를 설정했습니다.

• threshold의 값을 직접적으로 설정(SMD: 0.1)할 수도 있고, 비율로 설정(SMD: 0.5%)하는 방법이 존재하는데 후자를 선택하는 것이 더 실용적이라고 합니다.

결론

• 어노말 트랜스포머의 핵심 아이디어는 3가지로 정리할 수 있습니다
  • Reconstruction + Association Discrepancy criterion
  • Learnable Prior-Association
  • Minimax Strategy
• 위의 3가지 아이디어를 모두 결합했을때 최적의 성능을 얻을 수 있었으며, 특히 assocation-discrepancy에 사용되었던 아이디어는 시계열 데이터의 local/global 특성을 대조적으로 학습시키겠다는 것으로 이는 최근 발표된 다른 AD 모델에서도 적용된 아이디어입니다. 어노말 트랜스포머는 local 특성을 가우시안 분포로 모델링한다는 점입니다.
• 어노말 트랜스포머는 윈도우 사이즈가 작을 경우 성능이 안좋을 수 있는데, 윈도우 사이즈에 따라 연산량 증가가 많기 때문에 이를 적절히 조절해야 합니다.

• 최신 6개의 논문에서 사용된 Time Series 데이터셋 정리 및 모델 간의 성능 비교를 위해 작성
• 각 모델별 사용한 데이터의 특성, 모델의 특성이 다르기 때문에 해당 표는 단순히 참고용
• 논문 목록
  • Anomaly Transformer: Time Series Anomaly Detection with Association Discrepancy
    • Reconstruction-based method + Association Discrepancy loss를 추가
  • Time Series Anomaly Detection with Multi-resolution Ensemble Decoding
    • Reconstruction-based method + Multi-resolution 기법을 추가
  • Detecting Anomalous Event Sequences with Temporal Point Processes
    • Temporal point precess에서의 OOD detection을 AD로 해석
  • Neural Contextual Anomaly Detection for Time Series
    • Window 기법
  • Multi-Scale One-Class Recurrent Neural Networks for Discrete Event Sequence Anomaly Detection
    • OC-NN, event sequence + local, global latent space 를 따로 지정해 OC-NN을 수행
    • 로그 메시지를 미리 설정하여 이상현상을 찾아내는 모델
  • Multivariate Time Series Anomaly Detection and Interpretation using Hierarchical Inter-Metric and Temporal Embedding
    • 다변량 시계열 데이터를 2가지 관점에서 해석하여 각각을 임베딩하여 학습하는 모델
      • 하나의 변수 내에서 시간적인 변화량 관점
      • 여러 변수간의 상관관계 관점

데이터셋

(1) SMD (Server Machine Dataset, Su et al. (2019))

• 5-week-long dataset that is collected from a large Internet company with 38 dimensions.
• https://github.com/NetManAIOps/OmniAnomaly/tree/master/ServerMachineDataset
• https://gudwns1215.medium.com/how-to-time-series-anomaly-detection-using-deep-learning-edfc2d1dbbc8

(2) PSM (Pooled Server Metrics, Abdulaal et al. (2021))

• Multiple application server nodes at eBay with 26 dimensions.
• https://github.com/eBay/RANSynCoders/tree/main/data

(3) Both MSL (Mars Science Laboratoryrover) and SMAP (Soil Moisture Active Passive satellite)

• Public datasets from NASA (Hundman et al., 2018) with 55 and 25 dimensions respectively,
• Contain the telemetry anomaly data derived from the Incident Surprise Anomaly (ISA) reports of spacecraft monitoring systems.
• 데이터 확보가 어려워 일단 제외

(4) SWaT(Secure Water Treatment, Mathur & Tippenhauer (2016))

• Obtained from 51 sensors of the critical infrastructure system under continuous operations.
• https://itrust.sutd.edu.sg/itrust-labs_datasets/

(5) NeurIPS-TS (NeurIPS 2021 Time Series Benchmark)

• Proposed by Lai et al. (2021) and includes five time series anomaly scenarios categorized by behavior-driven taxonomy as point-global, pattern-contextual, pattern-shapelet, pattern-seasonal and pattern-trend.

(6) UCR Dataset

• Multi-dataset Time Series Anomaly Detection Competition of KDD2021.

(7) ECG

• This is a collection of 6 data sets on the detection of anomalous beats from electrocardiograms readings.
• https://www.cs.ucr.edu/~eamonn/discords/

(8) 2D-gesture

• This contains time series of X-Y coordinates of an actor’s right hand. The data is extracted from an video in which the actor grabs a gun from his hip-mounted holster, moves it to the target, and returns it to the holster. The anomalous region is in the area where the actor failsto return his gun to the holster.
• https://www.cs.ucr.edu/~eamonn/discords/

(9) Power-demand

• This contains one year of power consumption records measured by a Dutch research facility in 1997.
• https://www.cs.ucr.edu/~eamonn/discords/

(10) Yahoo’s S5 Webscope

• This contains records from real production traffic of the Yahoo website
• https://webscope.sandbox.yahoo.com/catalog.php?datatype=s

(11) RUBiS

• weblog dataset and was generated by an auction site prototype modeled after eBay.com
• User web behavior including user_id, date, request_inf

(12) Hadoop Distributed File Systme(HDFS)

• Generated by a Hadoop-based map-reduce cloud environment usingbenchmark workloads
• 11,175,629 log messages, of which 2.9% are labeled as anomalies by Hadoop experts

(13) BlueGene/L (BGL)

• 4,747,936 log messages generated by a BlueGene/L supercomputer system with 131,072 processors and 32,768 GB memory at Lawrence Livermore National Labs.

(14) WADI

• Water Distribution

(15) ASD

• Application Server Dataset
• https://github.com/zhhlee/InterFusion/tree/main/data